Each summer, undergraduate students have the opportunity to contribute to cutting-edge research with Department of Computer Science faculty.
The Natural Sciences and Engineering Research Council (NSERC) Undergraduate Student Research Award Program (USRA) and the University of Toronto Excellence Awards (UTEA) fund students to do 16 weeks of research with a professor over the summer.
With a wide range of faculty research interests across the department’s faculty, students have an opportunity to gain significant experience in an area of computer science that interests them.
Undergraduate students: interested in pursuing summer research opportunities in 2021? Apply by Friday, January 15.
Spanning graphics, computational linguistics, software engineering, and theory, here are four examples of projects from Summer 2020:
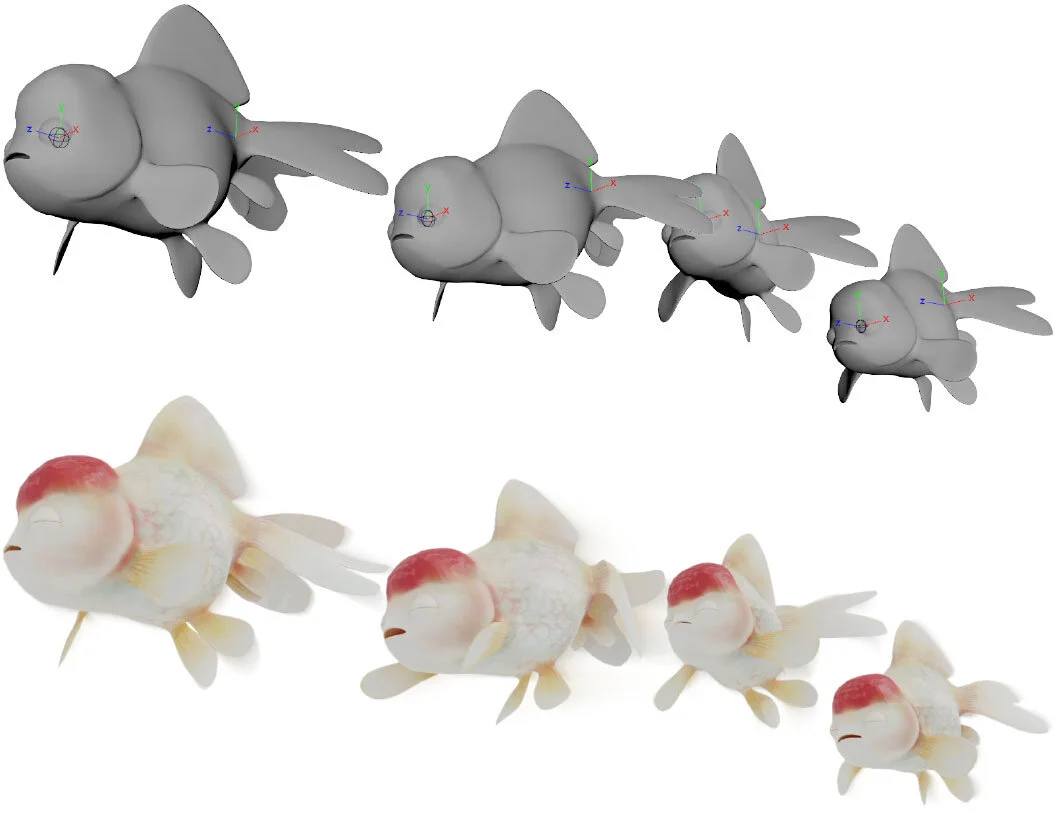
Complementary Dynamics
Faculty member: Alec Jacobson
Student: Jiayi Eris Zhang
Project description:
Animating characters is a lot of work. Trained artists work hard to get the general pose of the character where it should be, but it's still difficult to get secondary effects such as jiggling fat or wiggly appendages. Physically-based simulation can easily achieve these effects, but is not controllable by an artist. In Eris's work, she demonstrates how to have the best of both worlds. Artists control the general pose of a character while physical simulation controls high frequency, detailed effects. This way the artist and physics work in harmony.
Exploration of gender differences in COVID-19 discourse on Reddit
Faculty member: Suzanne Stevenson
Student: Jai Aggarwal
Project description:
Decades of research on differences in the language of men and women have established postulates about the nature of lexical, topical, and emotional preferences between the two genders, along with their sociological underpinnings. Using a novel dataset of male and female linguistic productions collected from a social media platform, we further confirm existing assumptions about gender-linked affective distinctions, and demonstrate that these distinctions are amplified in the emotionally-charged discourse related to COVID-19. Our analysis also reveals considerable differences in topical preferences between male and female authors in pandemic-related discussions.
Stress testing SMT solvers
Faculty member: Marsha Chechik
Student: Vaskar Nath
Project description:
Satisfiable Modulo Theory (SMT) solvers are important tools for many software engineering and programming language applications. These applications rely heavily on the correctness of SMT solvers, which makes bugs in the solvers critical. Inspired by the recent advancement in bug finding for SMTs solvers, we wish to explore new methods to identify “meaningful bugs” in SMT solvers and to provide insight to aid the solver repair.
The project evolves over three stages: (1) developing an automated technique to effective fuzz “meaningful” SMT test instances to find bugs in SMT solvers, (2) applying delta debugging techniques to minimize bug triggering test instances, and (3) analyzing solver execution traces on these bug instances to the isolate buggy solver components.
The end goal of this project is to establish a framework to stress test SMT solvers. The framework associates each discovered bug with a report including the minimized bug instances and the likely solver components that are responsible for the bugs.
We aim to evaluate the framework by (1) its bug finding efficiency (number of bugs per generated test instance), (2) its ability to minimize bugs, and (3) the accuracy and precision of the prediction for the buggy solver components.
Games with many entangled players
Faculty member: Henry Yuen
Student: Hugh Goatcher
Project description:
In quantum physics and quantum information theory, games with quantum entangled players have turned out to be an extremely useful tool with which to study quantum entanglement. These games have also led to many applications of quantum entanglement, ranging from quantum random number generation, verifiable quantum computing, and complexity theory. However, virtually all games that have been studied deal with only two players. The structure and behaviour of games with three or more players is virtually unknown; in this project, we aim to explore the properties of games with many entangled players. We use sophisticated theoretical and computational tools such as semidefinite programming and sum-of-squares proofs.
Header image source: Complementary Dynamics [PDF]